Linked Lists
What is a Linked List
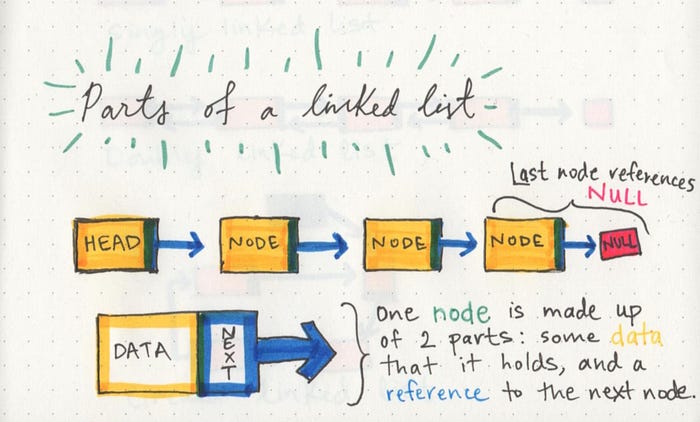
A Linked List is a sequence of Nodes that are connected/linked to each other. The most defining feature of a Linked List is that each Node references the next Node in the link.
There are two types of Linked List - Singly and Doubly.
- Singly - Singly refers to the number of references the node has. A Singly linked list means that there is only one reference, and the reference points to the Next node in a linked list.
- Doubly - Doubly refers to there being two (double) references within the node. A Doubly linked list means that there is a reference to both the Next and Previous node.
- Node - Nodes are the individual items/links that live in a linked list. Each node contains the data for each link.
- Next - Each node contains a property called Next. This property contains the reference to the next node.
- Head - The Head is a reference of type Node to the first node in a linked list.
- Current - The Current is a reference of type Node to the node that is currently being looked at. When traversing, you create a new Current variable at the Head to guarantee you are starting from the beginning of the linked list.
The best way to approach a traversal is through the use of a while() loop. This allows us to continually check that the Next node in the list is not null. If we accidentally end up trying to traverse on a node that is null, a NullReferenceException gets thrown and our program will crash/end.
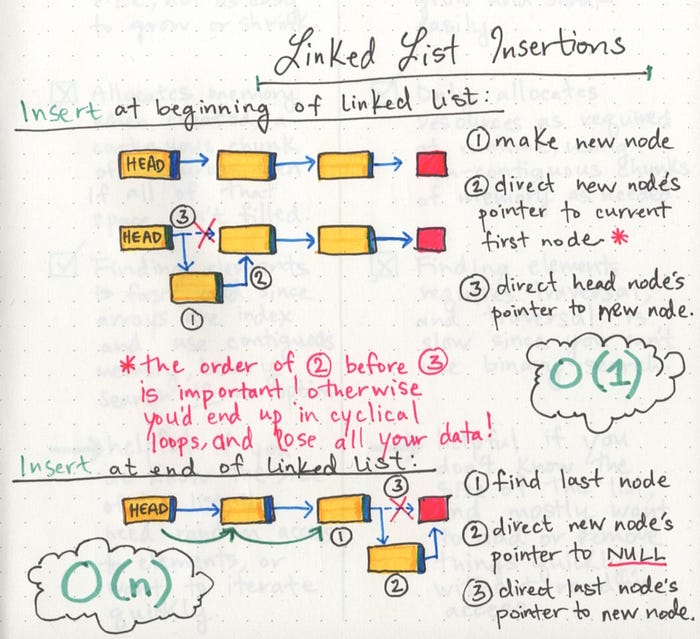
Adding a Node
Adding O(1) Order of operations is extremely important when it comes to working with a Linked List. What I mean by this is you must be careful that all references to each link/node is properly assigned.
If we want to add a node with an O(1) efficiency, we have to replace the current Head of the linked list with the new node, without losing the reference to the next node in the list.
When constructing your code, a few things to keep in mind.:When making your Node class, consider requiring a value to be passed in to require that each node has a value.
Linear data structures
If we really want to understand the basics of linked lists, it’s important that we talk about what type of data structure they are.
Memory management
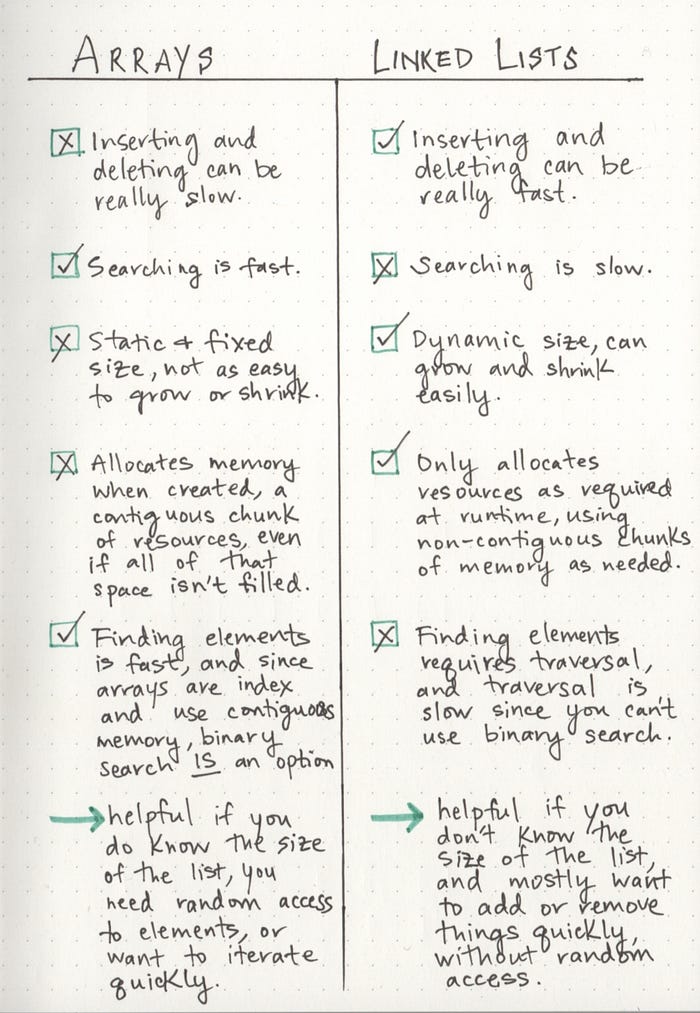
The biggest differentiator between arrays and linked lists is the way that they use memory in our machines. Those of us who work with dynamically typed languages like Ruby, JavaScript, or Python don’t have to think about how much memory an array uses when we write our code on a day to day basis because there are several layers of abstraction that end up with us not having to worry about memory allocation at all.

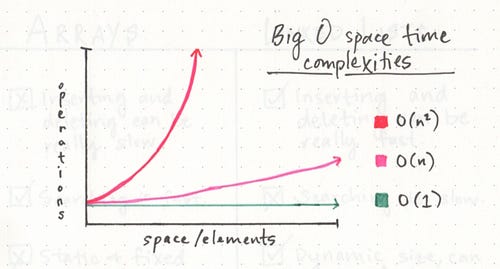
Big O Notation is a way of evaluating the performance of an algorithm.
One way to think about Big O notation is a way to express the amount of time that a function, action, or algorithm takes to run based on how many elements we pass to that function.
For example, if we have a list of the number 1–10, and we wanted to write an algorithm that multiplied each number by 10, we’d think about how much time that algorithm would take to multiply ten numbers. But what if instead of ten numbers, we had ten thousand? Or a million? Or tens of millions? That’s exactly what Big O Notation takes into account: the speed and efficiency with which something functions when its input grows to be any (crazy big!) size.
An O(1) function takes constant time, which is to say that it doesn’t matter how many elements we have, or how huge our input is: it’ll always take the same amount of time and memory to run our algorithm. An O(n) function is linear, which means that as our input grows (from ten numbers, to ten thousand, to ten million), the space and time that we need to run that algorithm grows linearly. For a little contrast, we can also compare these two functions to something starkly different: an O(n²) function, which clearly takes exponentially more time and memory the more elements that you have. It’s pretty safe to say that we want to avoid O(n²) algorithms, just from looking at that crazy red line!